Planar Defects – Grain Boundaries

In practice, metals (and indeed semiconductors) are polycrystalline and contain grain boundaries.

Lattice planes are not continuous across a grain boundary, and dislocation glide is impeded.

Grain size therefore affects the strength of a metal.

Larger grains mean softer material.

Grain boundaries are regions of poor packing, and hence are easy sites for vacancy diffusion to occur.

Diffusion will happen here more than in the bulk at low temperatures.

Can therefore identify two regimes of creep due to vacancy diffusion alone.

· Coble creep at low temperatures; grain boundary diffusion.

· Nabarro-Herring creep at high temperatures; bulk diffusion of vacancies.

Diffusion and Flow in Crystals

Model for bulk diffusion:

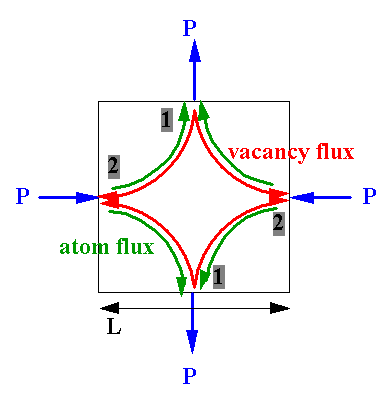
Imagine a cubic grain with population of vacancies under shear stress t, or equivalently stresses P shown.

No net change in volume. Atomic volume = W

Change in G_v = PW

At sites labelled 1 have net increase in vacancies and at 2 have decrease

Differences in populations lead to net flux of vacancies from 1 to 2 to remove gradient, and equivalently net flux of atoms from 2 to 1.

Concentration gradient ~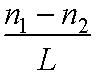

Flux J = Flow rate/unit area/unit time =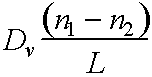

In unit time cube increases in thickness by JW

\strain rate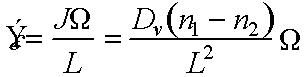

Now n₁- n₂~ n_eq2PW/kT for PW/kT<<1

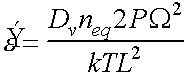
Now bulk diffusion coefficient D = D_v ´ n_eq/N

where n_eq/N is probability of vacancy site and 1/N=W

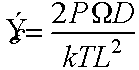
Other models give other prefactors.

Effective viscosity = =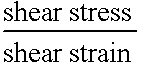

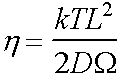
and is strongly grain size dependent.

e.g. for lead (M Pt ~600K)

Viscosity h in poises

T/K

L=1cm

L=10^-3cm

(polyXtal)

300

10²³

10¹⁷

595

10¹⁷

10¹¹

(1poise = 0.1 Pa s)

Grain Boundary or Coble Creep

In practice there must always be flow of grain boundaries to accommodate shape changes.

Because grain boundaries more disordered than bulk

D_gb>>D_bulk

Typically D_gb~ 10⁶D_bulk (although very hard to measure).

Contribution to creep from

grain boundary will be

d~ 1nm (ie few atoms layers are disordered); so for 1mm grain size d/L ~ 10^-6.

Contributions from N-H and Coble creep similar.

As grain size decreases Coble creep becomes more important.

Also true at low temperature when activation energy to create vacancies becomes an obstacle.

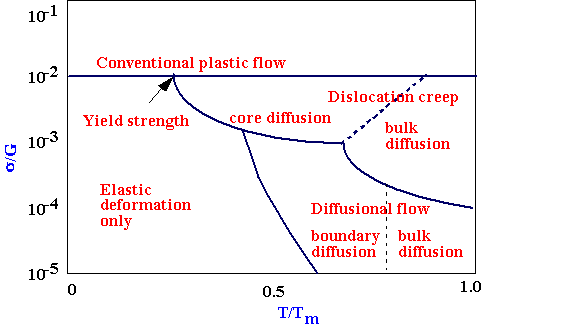
Ashby Deformation Map

These are a way of pulling all the ideas so far discussed together, taking into account the different regimes of behaviour.

Axes are normalised

Boundaries between different regimes will depend on strain rate and grain size.

Fracture

All materials show some elasticity.

Metals and many polymers also exhibit significant plasticity.

Fracture may occur with or without plasticity.

Brittle fracture is usually associated with rapid crack propagation without plastic deformation.

Ductile behaviour does have associated plastic deformation.

Arguments similar to those used to arrive at the concept of dislocations, show that the theoretical failure stress is much higher than that experimentally observed.

As before this is attributed to the presence of flaws: pre-existing cracks and stress concentrations.

Theoretical Strength

(Due to Orowan 1949, gives rough estimate)

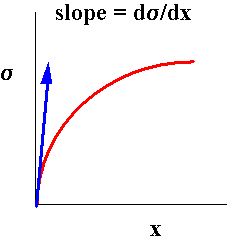
Assume stress-displacement relation of form

s = s_o sin [(p/a) (x-a_o)]

where a_o is equilibrium separation between planes

a is unknown distance, over which atomic forces act.

Initial slope can be related to Young's modulus.

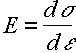and

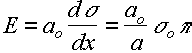for small x/a

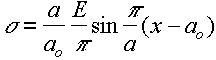substituting for s_o

Now a is not known, but Orowan evaluated it by equating the work done against the stress with the fracture surface energy g (note fracture produces 2 surfaces).

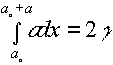
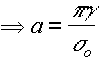
Hence theoretical breaking stress

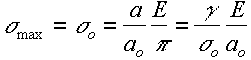
since a~a_o

In practice s_o much lower in general.

This is due to the presence of flaws such as pre-existing cracks and stress concentrations.

Stress Concentrations at Notches and Cracks

Inglis (1913) and Kolosoff (1914)

Imagine lines of force around a crack

Since crack cannot bear load, the lines of force become concentrated around the tips of the crack leading to a stress concentration.

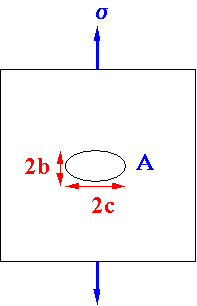
Consider elliptical hole in plate under uniform tension s.

Crack tip radius

r =b²/c

Stress concentration a maximum at A, and can be shown to be

Usually have c>>r; then

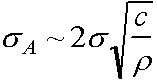
For circular hole b=c and s_A = 3s acting tangentially.

As r decreases (ie crack gets sharper), stress concentration increases.

Eg c=10µm, r = 0.5nm (ie atomically sharp)

s_A/s ~ 300

Stress falls off very fast ahead of crack tip within distance ~c.

Crack can be surface notch or step (in which case c is the total notch length).

Griffith Criterion

This criterion expresses when a pre-existing crack is likely to lead to crack propagation and hence fracture.

It is an argument based on energy balance.

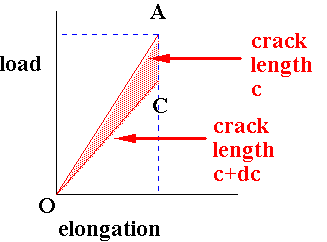
Energy released = area of DOAC

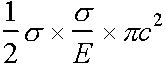~ for unit thickness

(approx for sphere)

strain

More accurate calculations lead to

Energy U =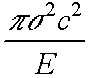

As crack grows

Griffith criterion says the crack will advance catastrophically if more energy is released than that absorbed by crack growth (W) due to creation of new surface

W = 2c 2g = 4cg

i.e

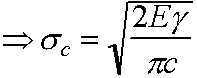Griffith criterion

Can also be expressed in terms of

G = elastic energy release rate, or crack driving force

(where the use of the word rate means per increment of crack length not time)

G has dimensions of energy/unit plate thickness/unit crack extension

Two crack tips

2G = dU/dc = dW/dc = 4g

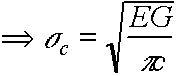
Strong materials have high E and g, and small c.

But strong is not the same as tough.

Tough materials imply large energy absorption as crack advances i.e. large G or dW/dc or g.

Note energy released µ c²

But energy absorbed µ c

Critical condition must always be met for large enough crack, but may not be for small specimen with small cracks.

Fracture Mechanics

When a block containing a crack is stressed, there is a stress concentration at the crack tip which falls off with distance.

The stress at any point (away from the actual crack tip where a singularity would be implied) can be writtne

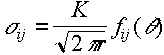q = azimuthal angle

r= distance ahead of tip

K is the stress intensity factor – it depends on crack length, applied stress and specimen geometry.

specimen geometry dependent term

K is a link between detailed stress field around crack and 'macroscopic' quantities such as applied stress and crack length.

Modes of Loading

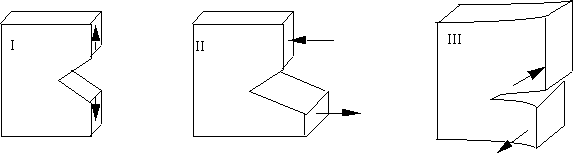
For the simple case of mode I loading of crack of length 2c

Recalling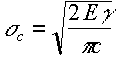

Critical stress intensity factor

For mode I loading

Note this provides a way to measure g for brittle material, by finding the value of K_Ic ie introduce notch of known length c, and find critical stress.

However many materials do not simply show brittle failure, and there may be extensive crack tip plasticity.

Existence of this plasticity removes the stress singularity at the crack tip.

Energy absorption is then much greater, and appropriate g will not simply be surface energy.

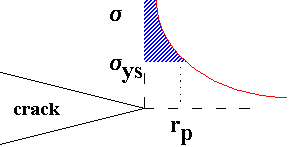Simplest model assumes deformed zone of radius r_p ahead of crack tip within which stress = yield stress s_ys

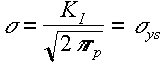
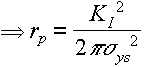and

In fact this is underestimate, since load indicated by shaded area must still be supported and hence stress beyond circular zone pushed up so more deforms.