Obstacles to Dislocation Motion
Many objects can impede dislocation motion:
\ Other dislocations
\ Precipitates
\ Grain boundaries
Dislocation Interactions
When dislocations intersect, jogs and kinks are formed.
A kink is a step in the dislocation line in the slip plane:
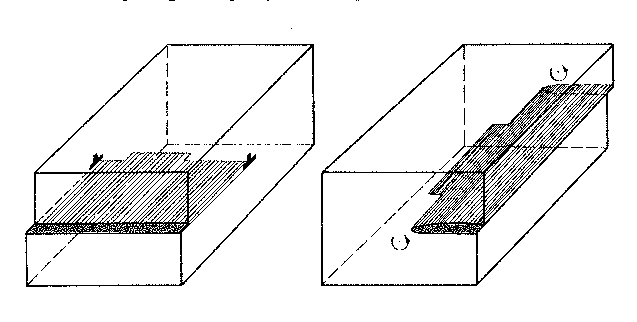 A kink in an edge dislocation (left) and a screw
dislocation (right).
A kink in an edge dislocation (left) and a screw
dislocation (right).
A jog is a step in the dislocation line onto another slip plane:
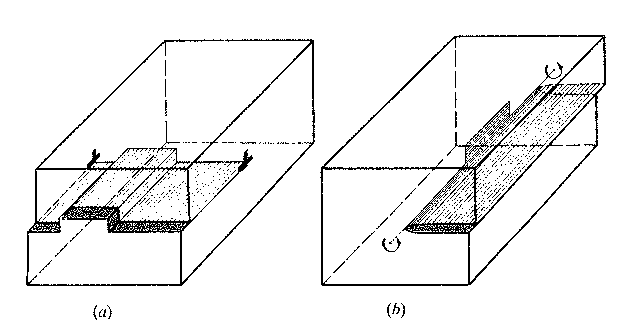
A jog in an edge dislocation (left) and a screw dislocation (right).
A kink, lying in the slip plane provides no impediment to motion.
This is the case when edge dislocations meet.
But if a jog with edge character is formed in a screw dislocation it cannot glide since the glide plane for the jog is different from that for the main dislocation line.
In the case illustrated of a jog introduced by a screw intersecting with either another screw or an edge dislocation, the jog has edge character and a different glide plane.
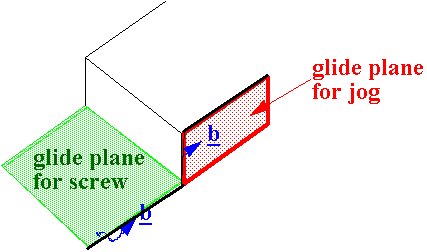 |
The jog is pinned and the dislocation is said to be 'sessile'.
In this case motion can only occur by the dislocation line moving out of its existing glide plane – this is known as non-conservative motion; the length of the dislocation line is not conserved.
(Motion on the glide plane is known as conservative).
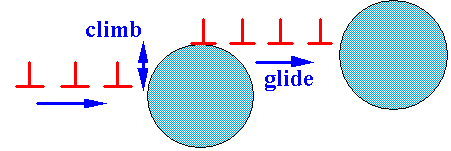
Climb – Diffusion-Controlled Creep
Dislocation climb allows dislocations to climb round obstacles which are impeding their glide, thus allowing slip to continue.
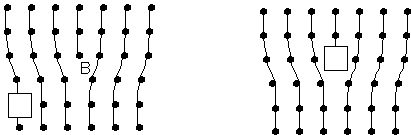
A vacancy diffuses to the position of atom B, causing the dislocation to climb one lattice vector.
Diffusion can occur either through the bulk of the crystal - as shown ('lattice diffusion') - or along the dislocation core ('pipe diffusion').
This non-conservative dislocation mechanism gives rise to high temperature creep deformation.
It only occurs at comparatively high temperatures because of the temperature dependence of the diffusion.
It is a means of unpinning sessile dislocations.
Rate of Climb and Stress Dependence
This process also allows dislocations to climb round precipitate particles.
In this case the rate of creep is determined by the rate at which dislocations
can climb past obstacles.
 |
How do dislocations respond to a stress t?
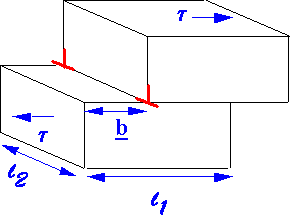 |
Consider this stress causing a dislocation to move right through a crystal of size l1
External work done dW = t ´ l1 ´ l2 ´ b
stress area displacement
Also dW = force on dislocation/unit length
´ length ´distance travelled
= f ´ l2 ´ l1
Ž f = t b
Now at a precipitate particle
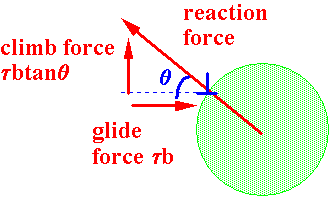 In
equilibrium:
In
equilibrium:
Reaction force = glide + climb force
Climb force = tb tanq
Hence increases with stress
As shear stress increases, more dislocations unlocked and more creep occurs.

Situation usually described by
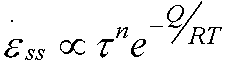
and known as power law creep.
This also has strong T dependence, requiring vacancy diffusion.
Multiple Cross Slip
Screw dislocations do not have a unique glide plane.
Thus for them (but not for edge) an alternative way to get round obstacles is available, known as multiple cross slip.
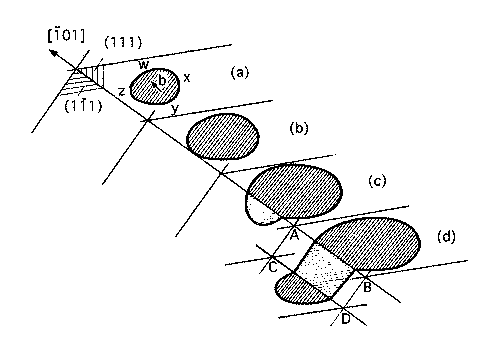
Cross-slip in
a face-centred cubic crystal: A screw
dislocation at z can glide in either the (111) or the (![]() ) close-packed planes.
) close-packed planes.
Multiple cross-slip occurs in (d), as it moves from one plane to the other, and then continues to move parallel to the first glide plane.
Energy of a Dislocation
Consider the case for a screw dislocation
 |
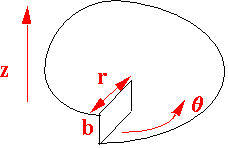
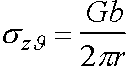
(stress = modulus ´ strain)
This is the stress acting in the z direction across plane q = const.
\ energy = 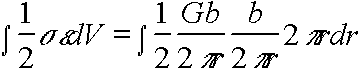 /unit length
/unit length
The upper limit of the integral, R, is given by the distance to nearest dislocation of opposite sign/loop diameter.
The lower limit ro represents the inner cut-off where linear elasticity breaks down.

Energy = 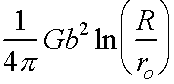 /unit length
/unit length
For edge dislocations, the effect of Poisson's ratio n has to be taken into account.
Etot = 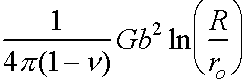 / unit length
/ unit length
Including core energy
Etot ~ 1/2 Gb2 - a few eV/atom plane
(of which ~10% is core).
Dislocations are not usually in thermal equilibrium, so some means must be found to create them.
Production of Dislocations
Example: Frank Read Source – dislocation pinned at both ends.
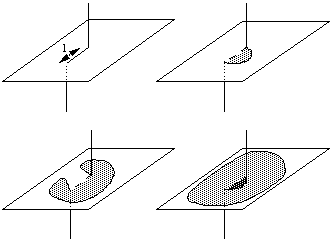
What is the force on the curved segment causing it to bow out?
Line tension T can be equated to energy/unit length.
\ T ~ 1/2 Gb2
For curved segment
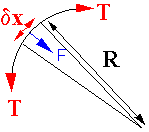 Total normal force on
segment
Total normal force on
segment
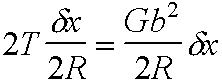
If in equilibrium with applied stress,
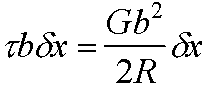
 |
\ 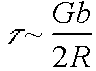 or
or 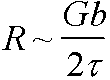
i.e equilibrium radius of curvature is controlled by stress.
The Frank Read source expands under the stress, pinned at both ends.
When the bowed dislocation line reaches a semicircle it can continue to expand under a diminishing force.
There are other sources of dislocation lines:
\ single Frank-Read sources, where the line is pinned only at a single source.
\ Intersections with other dislocations – jogs increase the length of the line , and may act as Frank Read sources.
Regimes of Deformation
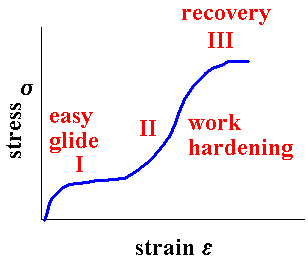
I Easy Glide – only one slip system operates: single crystals only
II Work hardening – multiplication and interaction of dislocations
III Dynamic recovery, - multiple cross slip, climb and polygonisation.
Polygonisation allows random dislocation arrays to rearrange to reduce strain energy.
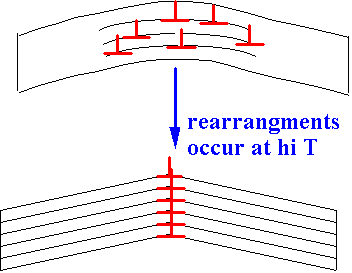 |
Both climb and glide required: facilitated by high T and stress.
Low angle grain boundaries tend to form as a result.
Precipitation Hardening
Pure metals tend to be very soft.
Second phase particles (precipitates)
are often added to toughen them, by impeding dislocation motion.
1)

The dislocation line is in tension, and as it meets each particle will exert a force on it.
2)

The dislocation line has to bow round the particles.
To progress further either A) the particles have to be cut through or B) the line may curve so much around each particle it forms a loop (Orowan looping).
The force for each process can be calculated, so that it can be deduced which process will dominate.
A) Cutting

B) Orowan looping


In order to optimise the toughening impact of precipitates, their size and spacing must be controlled.
Cutting Force
If one particle is cut through the dislocation line advances a distance h.
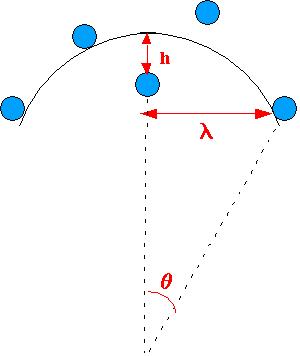 l is mean distance between particles along
line.
l is mean distance between particles along
line.
lo is average interparticle spacing
Area swept out when one particle is cut through ~hl, which must be approx equal to lo2
solo2 ~ h l
For small q h/l ~ sinq Ž (lo/l)2 ~ sin q
Critical cutting force Fc = 2T sin q
Ž Fc =2Tlo2/l2 or l
~ lo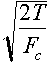
Cutting force depends on distribution of precipitate particles.
Can now substitute for T
2Tsin q = tbl (since line length l before cutting) and this must equal force on each particle.
\ critical stress for cutting tc = Fc/bl
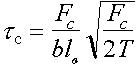 and T ~
1/2 Gb2
and T ~
1/2 Gb2
 |
\ 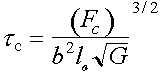
In contrast if looping occurs
 |
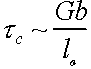
Thus cannot simply add tougher and tougher particles to strengthen material, since if Fc too big, will get looping instead.
In general there is an optimum dispersion with particles not too big (typically cutting force µ particle radius (Fc =kr) and not too far apart.
Particle size Effect on Yield Stress
If an alloy has a fixed volume fraction of strengthening particles, is it better to have fine, closely spaced particles, or coarser, more widely spaced particles?
Consideration of the critical stresses for cutting and looping shows that there is an optimum particle size for precipitate hardening.
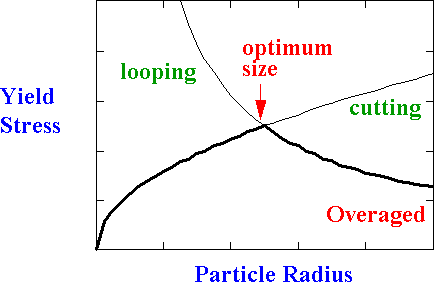 |
During long term service, annealing may occur leading to coarsening of particles.
In this case strength may drop over time, and can set a useful working life on e.g. a turbine blade.