AMORPHOUS SOLIDS

Books

Introduction to Glass Science and Technology, J E Shelby, RSC 1997

Soft Condensed Matter, R A L Jones, OUP 2002

Physics of Amorphous Solids, R Zallen 1998

The Structure of Materials, S M Allen, EL Thomas, Wiley 1999

Insulating and Semiconducting Glasses, editor P Boolchand, World Scientific, 2000.

In addition there are some useful out of print books, probably to be found in some colleges, as well as the department library:

Glasses and the Vitreous State, J Zarzycki CUP 1991

Physics of Amorphous Materials, SR Elliott, Longmans

N.B. Very few books deal with this topic satisfactorily, so I will give out more comprehensive notes on the amorphous state than for other parts of the course.

Introduction

There are many ways in which a material can deviate from the regular packing of a crystal.

Amorphous materials - solids and liquids - differ from crystals in that they do not possess long range periodicity of packing.

They will therefore be isotropic.

Window glass - basically SiO₂ - is a common example.

Many plastics (perspex, uPVC) are also amorphous.

However both metal alloys and semi conductors can also be made amorphous by appropriate processing routes.

Amorphous materials exhibit a glass transition upon cooling from the melt.

Understanding the nature of the glass transition is not yet complete at a theoretical level.

Characteristics of the Glass Transition (T_g)

· Well above T_g the material flows

Material is in thermal equilibrium; properties determined by two external parameters e.g. P.T.

· Well below T_g, properties similar to a crystalline solid

(in terms of density, enthalpy etc).

· Essentially no viscous flow; high shear modulus.

However the glass is not in thermal equilibrium.

· At least one internal parameter is required to define it, although this may be hard to identify.

So what happens around the glass transition temperature, T_g?

Around T_g

Changes in volume (V), enthalpy (H) and entropy (S) are continuous, but have a change in slope at T_g.

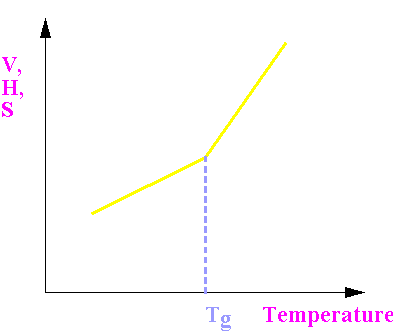
This means their derivatives such as Cp (µ dS/dT) and

a (µ dV/DT) are discontinous.

It resembles a 2^nd order transition.

However the glass transition is not a true thermodynamic

(2^nd order) phase transition.

The temperature T_g is not fixed but depends on experimental conditions, particularly the cooling rate.

Glass 1 cooled faster than glass 2, and deviates from equilibrium supercooled line at higher temperature.

Cool more slowly and Tg (temperature at which discontinuity in V seen) drops to lower temperature for glass 2.

Glass 2 can stay in equilibrium longer, and therefore stays on supercooled line further.

The net effect is that Tg₂ < Tg₁.

Practically, Tg can be found by looking at the heat capacity.

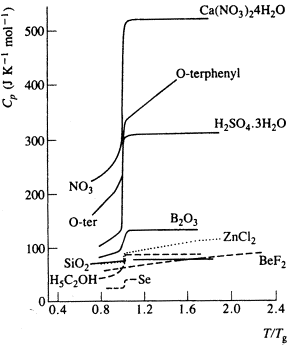
The diagram shows normalised heat capacity measurements for a range of inorganic glasses.

In each case there is a significant step change in C_p at the glass transition temperature.

From such curves can extract the entropy since

· Clearly entropy in the glass varies with cooling rate too.

· The entropy in a glass is not zero at absolute zero.

· How much residual entropy there is depends on how much configurational disorder there is - and this depends on cooling rate.

Tg occurs when the timescale of molecular rearrangements are too long for equilibrium to be maintained.

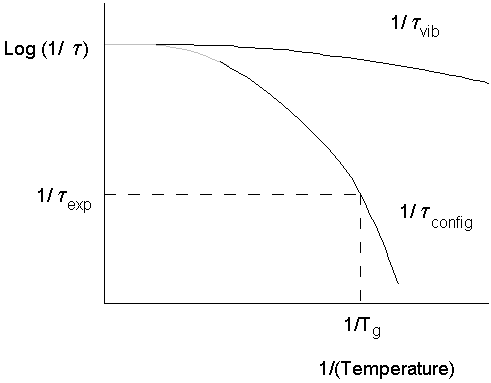
· This means the timescale of the experiment matters.

· A high/frequency/short timescale experiment allows less long for equilibrium to be established - even for an identical cooling rate.

· So NMR (high frequency technique 10¹⁵ Hz) always measures a higher Tg than DSC (differential thermal calorimetry, 1Hz)

· In the glass itself, Cp is similar to the crystal, and originates in vibrational modes which are still present.

· Long range translational motions are frozen out.

Kauzmann Paradox

T_g decreases as melt cooled more and more slowly.

What happens for a system cooled infinitely slowly?

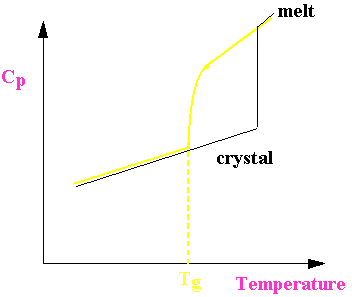
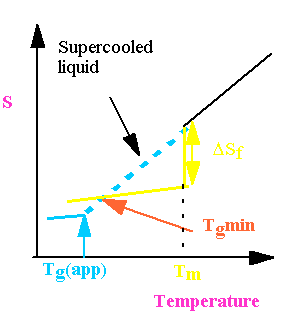
Therefore

=

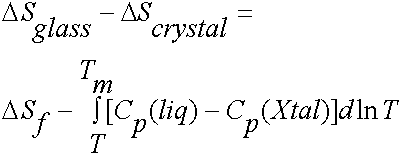
where DS_f is the entropy of fusion.

Now we would not expect to be negative, (ie we expect the entropy in the glass to be greater than in the crystal).

Therefore there is a lower bound for T_g given by the equation

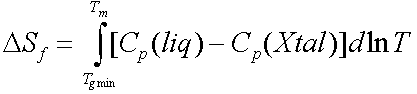
However slowly you cool T_g cannot fall below this value.

The Kauzmann paradox is that apparently if you cool slowly enough it ought to be possible to achieve an entropy in the glass which is the same, or even lower, than the crystal.

This is still a hotly debated topic amongst theoreticians in this area.

Relaxation Times and Viscosity

By the temperature T_g configurational relaxations (including translational motion) are frozen out, but vibrational relaxations are still in equilibrium.

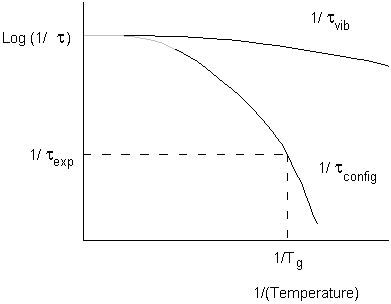
When the timescale of the experiment and the configurational relaxation time coincide, we begin to see departure from equilibrium.

This identifies T_g for the particular experiment being used.

The timescale for configurational relaxation will be related to rotational or translational diffusion coefficients.

These in turn relate to viscosity.

(Note operational definition of T_g is when the viscosity of the supercooled liquid exceeds 10¹³ N s m^-2)

Whereas in the liquid there is an Arrenhius type (ie with a Boltzmann factor containing an activation energy) dependence of the viscosity on temperature, this is not the case around the glass transition.

In many systems the so-called Vogel-Fulcher law is followed.

where h_o and B are constants.

This goes to infinity at T=T_o, which is usually about 50K below experimental T_g's.

Can one predict the Vogel-Fulcher Law?

This requires theories of the glass transition, which are not fully resolved.

Theories of the Glass Transition

1) Simplest model is the so-called Free Volume Theory – widely used, particularly in the area of polymers.

Conceptually simple, and can be useful, but cannot be rigorously correct!

Envisages there being 'free volume' into which atoms may jump to permit motion.

The amount of free volume is temperature dependent:

V_f =V_fg +a_v(T-T_g)

Where V_fg is the free volume at T_g and a_v is related to the difference in glass and liquid expansion coefficients.

Then

where V_o is the volume actually occupied.

Hence the Vogel-Fulcher law follows.

The theory is unfortunately based on physically unrealistic assumptions and cannot, for instance, predict the correct pressure dependence of h, but is nevertheless widely used in the study of viscoelastic phenomena (see later).

2) Mode Coupling Theories

Mathematically much more complex, but still no more widely accepted than previous 'theory'.

In the glass there are density fluctuations, which can be expressed in terms of damped density waves.

When considering the decay of the density-density correlation function, different modes are not independent,

i.e. they are coupled.

A consequence is that there is a divergence for the relaxation time for density fluctuations, and in turn the viscosity diverges as a power law.

Thus this model, which must have some truth in it, cannot predict the Vogel-Fulcher Law.

3) Exactly soluble models

This is a general approach in theoretical physics – try to find an exact solution to one specific form of the problem to try to understand the general physics underlying the general form of the problem.e.g. Edwards and Vilgis 1986 Physica Scripta

Considered a system of rods on a lattice

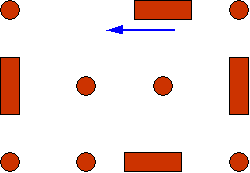
Rods can only move along their length, and until they hit an obstacle.

As T drops, packing density goes up and rods are more likely to bump into other rods.

As T_g approached, motion of individual rods becomes impossible, but cooperative motion is possible.

Number of rods which need to be involved in such cooperative motion gets larger and larger as T drops further (so is akin to mode coupling theories).

This can predict the Vogel-Fulcher Law.

Can you Change the Structure of a Glass?

Yes – although it is a non-equilibrium structure, it is possible to 'anneal' the glass, to encourage it to move towards equilibrium.

Thus a glass may 'densify' upon annealing, as it moves to a more nearly equilibrium state. (For optical components, such annealing permits strains to be removed, making the glass more uniform – known as stabilisation.)

Convenient to introduce the 'fictive temperature' – the temperature at which the glass would be in thermal equilibrium.

In other words T_f is the equilibrium temperature of the liquid at the moment of solidification in an idealised sense.

The slow cooled glass has fictive temperature T_{f 2} and the fast cooled T_{f 1} in the above diagram.

Since the fictive temperature depends on rate of cooling, if you cycle a glass, cooling at one rate and heating at another, can get hysteresis effects.

Cool slowly and reheat fast.

System cannot keep up with fast heating rate, so response falls behind until T_g2 passed. Then get overshoot.

This can be seen in DSC experiments.

Types of Glass

Type Use

Oxide (inorganic)

SiO₂, (window glass) Structural and optical

B₂O₃, GeO₂ etc

Amorphous semiconductors Electro-optical

a-Si, a-Ge Solar Cells

Chalcogenides Electro-optical

S, Se, As-Se Xerox machines

Metals Magnetic materials

Often complex stoichiometries Casette recording heads

And may involve metalloids (soft magnetically but wear

e.g Fe-B resistant)

Organic Materials Food- boiled sweets

Glycerol, sugar solutions Ice cream matrix

Polymers Optical (PMMA)

Structural (PS, PVC)

Preparation of Glasses

In general trick is to cool sufficiently fast to avoid crystallisation.

How fast is required depends on system.

System Necessary cooling rate

Amorphous (atactic) polymers Cannot crystallise

SiO₂ 10^-4K s^-1

Metallic alloys 10⁵ K s^-1

a-Ge, a-Si 10⁸ K s^-1

In general rate of crystallisation a maximum at T/T_m~ 0.8.

Also depends on h.

So materials with a high h at T/T_m~ 0.8 can most easily form glasses – this is the case for SiO₂.

Practical Methods for Achieving Rapid Quenching

1) Droplets of metal may be fired at high velocity onto cooled plate – 'splat quenching'

2)

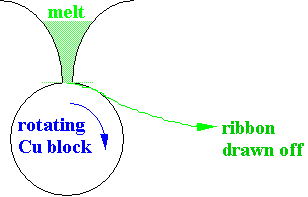
Continuous melt spinning

· Thin tapes, 20-50µm may be made this way.

· Typical quench rate ~10⁵ K s^-1.

3) Thermal evaporation in a vacuum

· Material is evaporated onto a cold substrate.

· Vacuum needed to prevent contamination, but even so reproducibility between samples may not be so good.

· a-Si and a-Ge often produced this way.

· Obtain a thin amorphous film

4) Pressure induced amorphization

· This is a solid-phase transition, which can occur at high pressure but low temperature.

· eg crystalline ice transforms to a-ice at 77K for P>10kbar.

· Presence of shear also useful, and ball milling can be used to produce amorphous alloys.

Structural Characterisation of Amorphous Materials

(These methods will also apply to liquids)

Just as diffraction is very useful for crystals, so it is (strictly speaking scattering) for amorphous materials. X-ray and neutron scattering most commonly used.

Principles similar, but no longer have sharp Bragg peaks, so have to think carefully about what information can be extracted from an experiment.

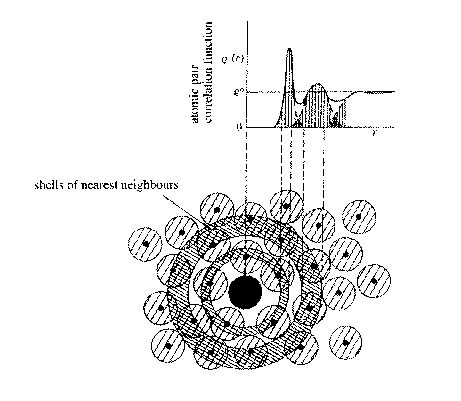
The radial distribution function (RDF) g(r) is defined as the number of atoms lying between r and r+dr of the centre of any given atom.

g(r) = 4πr²r(r)

where r(r) is the atomic pair correlation function:

r(r) = 0 for r < nearest neighbour separation

r(r) = r₀ average density at large r.

In between there are oscillating peaks corresponding to most probable distance for finding 1^st nearest neighbour, 2^nd nearest neighbour etc.

These nearest neighbour positions similar to those in a crystalline solid.

Scattering Experiment

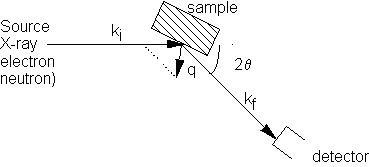
In general for an assembly of atoms, the intensity of scattering I is equal to the sum of the scattered amplitudes from each atom, multiplied by its complex conjugate.

Scattered intensity I given by

I = f_m expiq.r_m f_n exp- iq.r_n

where q is the scattering vector (k_f- k_i) and f_m,n are the atomic scattering vectors for atoms at sites r_m, r_n.

For an isotropic material this can be spatially averaged:

I = f_mf_n expiq.r_mn where r_mn= r_m - r_n

and <expiq.r_mn>= where |q| = q =

Then I = f_mf_n = f² + f_mf_n

This can be rewritten in terms of an integral using r(r).

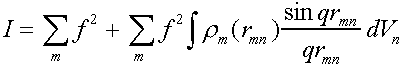
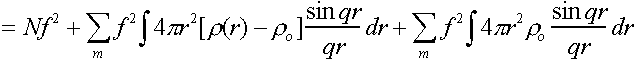
(N is number of atoms in the sample).

In general last term corresponds to interactions between far distant scattering centres, and hence to very low angle scattering which can usually be ignored.

and [r(r)-r_o] is only non-zero for smallish r, so limits of integration can conveniently be taken as 0,∞.

Now define structure factor S(q)

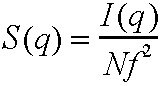
such that it can be obtained from experiment.

Then S(q)-1 =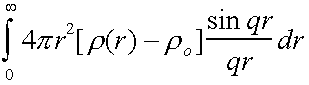

Which can be inverted to give

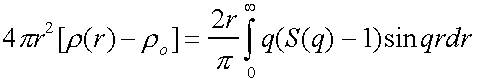
= g(r) – 4πr²r_o

So the radial distribution function can be obtained from a scattering experiment.

This can be a sensitive test of models for structure, though more widely applied to liquids so far than glassy structures.

Computer modelling approaches are now frequently used to simulate data.

Earlier physical constructs were used.

1) Aggregates formed from ball bearings in a bag, squeezed together to maximise packing, and then glued.

Measurements were then made on this 'dense random packed' model, pioneered by Bernal.

2) Continuous random networks can be formed for covalently bonded atoms – see model in Museum.

Note r.d.f's can be extracted from the models and compared with experiment.

3) Monte Carlo techniques (computer modelling).

· Starting structure chosen as a 'best guess'.

· Randomly selected atom given random displacement.

· If fit to r.d.f. improved, the move is accepted.

· Otherwise the probability of acceptance governed by Boltzmann distribution function.

· Continue making moves until result adequately close to experiment.

4) Molecular dynamics approach (this allows dynamic processes to be studied, unlike other methods; another computer modelling approach).

· Small number of atoms (~100-1000, possible maximum increasing with size of computer) confined to a box with periodic boundary conditions.

· Potential energy between atoms simulated by appropriate pair potential, eg Lennard Jones.

· Atoms initially given random positions and velocities.

· Equations of motion for position and momenta are then solved after successive time steps ~10^-14s.

This can be used to study how structure evolves as a liquid is cooled into a glass, although the effective cooling rate in such a simulation is often very high.